หน่วยการเรียนรู้ที่ 3

หน่วยการเรียนรู้ที่ 3    ข้อมูลในเครื่องคอมพิวเตอร์

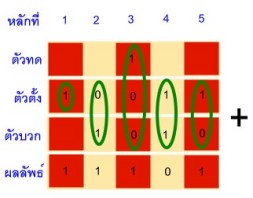
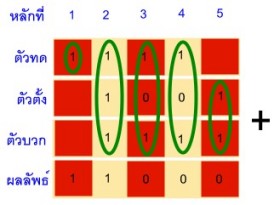
 คอมพิวเตอร์ทำงานด้วยหลักการทางอิเล็กทรอนิกส์ที่ใช้สัญญาณทางไฟฟ้าแทนตัวเลขศูนย์และหนึ่ง ซึ่งเป็นตัวเลขในระบบเลขฐานสอง แต่ละหลักเรียกว่าบิต (binary digit : bit) และเมื่อนำตัวเลขหลายๆ บิตมาเรียงกัน จะใช้สร้างรหัสแทนจำนวน อักขระหรือสัญลักษณ์ทั้งภาษาไทยและภาษาอังกฤษได้ และเพื่อให้การแลกเปลี่ยนข้อความระหว่างมนุษย์กับคอมพิวเตอร์เป็นไปในแนวเดียวกัน จึงมีการกำหนดมาตรฐานรหัสแทนข้อมูลในระบบเลขฐานสองขึ้น โดยรหัสมาตรฐานที่นิยมใช้กันมากมีสองกลุ่ม คือ รหัสแอสกีและรหัสเอ็บซิดิก

2.3.1 ระบบเลขฐานสอง      ในชีวิตประจำวันของมนุษย์ต้องได้พบเจอกับจำนวนและการคำนวณอยู่ทุกวัน หากเราสังเกตจะพบว่าจำนวนที่เราคุ้นเคยอยู่ทุกวันนั้นไม่ว่าจะเป็นการซื้อของเป็นเงิน 39,587 บาท จำนวนเงินฝากในธนาคาร 1,426,000 บาท หรือจำนวนในใบแจ้งหนี้ค่าโทรศัพท์จำนวน 2,560 บาท ล้วนแล้วแต่ประกอบขึ้นจากตัวเลข 10 ตัว คือ 0,1,2,3,4,5,6,7,8 และ9 ทั้งสิ้น ตัวเลขทั้ง 10 ตัวนี้ถือได้ว่าเป็นเครื่องมือที่ช่วยในการนับจำนวนของมนุษย์ การที่มนุษย์เลือกเลข 10 ตัวในการแทนการนับ อาจเนื่องจากมนุษย์มีนิ้วมือที่สามารถใช้เป็นอุปกรณ์ช่วยนับได้เพียง 10 นิ้ว จึงกำหนดระบบตัวเลขนี้ขึ้นมาและเรียกว่า ระบบเลขฐานสิบ (decimal)
		ต่อมาเมื่อมีการใช้งานคอมพิวเตอร์ซึ่งเป็นอุปกรณ์อิเล็กทรอนิกส์ที่ทำงาน      แบบ ดิจิทัลและใช้ระดับแรงดันไฟฟ้าแสดงสถานะเพียง 2 สถานะ คือ ปิด       (แทนด้วย 0) และเปิด (แทนด้วย 1)
	หรืออาจกล่าวได้ว่าเครื่องคอมพิวเตอร์รู้จักตัวเลขเพียง 2 ตัวเท่านั้น คือ 0 และ 1 หากมนุษย์ต้องการใช้คอมพิวเตอร์เป็นเครื่องมือช่วยทำงาน มนุษย์ต้องเรียนรู้ระบบเลขที่ประกอบด้วยตัวเลขเพียง 2 ตัวเช่นกัน จึงได้มีการคิดค้นระบบเลขฐานสอง (binary) ขึ้นเพื่อช่วยในการสื่อสารกับเครื่องคอมพิวเตอร์ โดยระบบเลขฐานสองเป็นระบบตัวเลขที่ประกอบด้วยตัวเลขเพียง 2 ตัว คือ 0 และ 1 เท่านั้น ตัวอย่างเลขฐานสอง เช่น 1102 , 101102

                     นอกจากระบบเลขฐานสองแล้ว ในการทำงานของคอมพิวเตอร์ยังอาจเกี่ยวข้องกับระบบตัวเลขระบบอื่นอีก เช่น ระบบเลขฐานแปดและระบบเลขฐานสิบหกซึ่งระบบเลขฐาน ทั้งสองจะมีแนวคิดในทำนองเดียวกันกับระบบเลขฐานสองและฐานสิบ กล่าวคือระบบเลขฐานแปดก็คือระบบเลขที่ประกอบด้วยตัวเลขเพียง 8 ตัว คือ 0,1,2,3,4,5,6, และ 7 ตัวอย่างเลขฐานแปด เช่น 1673₈ 76513₈ ในขณะที่ระบบเลขฐานสิบหกนั้นจะประกอบด้วย ตัวเลขทั้ง 10 ตัวที่ใช้อยู่ในระบบเลขฐานสิบ และเพิ่มตัวอักขระภาษาอังกฤษ A , B , C , D , E และ F แทนจำนวน 10 11 12 13 14 และ 15 ตามลำดับ ตัวอย่างเลขฐานสิบหก เช่น A1549₁₆ F7DA2₁₆ 8743₁₆

      จากที่กล่าวมาข้างต้น จะเห็นว่าการเขียนเลขฐานสอง ฐานแปดและฐานสิบหกนั้น มักจะเขียนตัวเลข 2 8 และ 16 กำกับอยู่ที่ตัวสุดท้าย ทั้งนี้เพื่อป้องกันความสับสน เช่น 8743 หากเราไม่เขียนตัวเลขกำกับไว้ ตัวเลขนี้อาจเป็นเลขฐาน 10 หรือฐาน 16 ก็ได้เราก็จะไม่ทราบว่าตัวเลขที่เขียนนั้นเป็นเลขฐานใด

ารางด้านล่างนี้เป็นตารางแสดงค่าของตัวเลขในระบบเลขฐานทั้งสี่ระบบที่กล่าวถึงข้างต้น ตารางแสดงรูปแบบของเลขในฐานสอง ฐานสิบ ฐานแปด และฐานสิบหก
	เลขฐานสิบ เลขฐานสอง เลขฐานแปด เลขฐานสิบหก 0 0000 0 0 1 0001 1 1 2 0010 2 2 3 0011 3 3 4 0100 4 4 5 0101 5 5 6 0110 6 6 7 0111 7 7 8 1000 10 8 9 1001 11 9 10 1010 12 A 11 1011 13 B 12 1100 14 C 13 1101 15 D 14 1110 16 E 15 1111 17 F

(1) การแปลงเลขฐานสิบเป็นฐานสอง
      คำศัพท์ที่จำเป็นต้องทำความรู้จักเพื่อให้เข้าใจตรงกันในการดำเนินการต่างๆ ในระบบเลขฐานสองมีดังนี้
            (ก) บิต (bit) คือหลักแต่ละหลักในระบบเลขฐานสอง เช่น 110₂ ประกอบด้วย 3 บิต
            (ข) บิตที่มีนัยสำคัญสูงสุด (most significant bit : MSB) คือบิตที่อยู่ซ้ายมือสุดเป็นบิตที่มีค่าประจำหลักมากที่สุด เช่น 100₂ บิตที่มีนัยสำคัญสูงสุดคือ 1 มีค่าประจำหลักเป็น 2²
            (ค) บิตที่มีนัยสำคัญต่ำสุด (least significant bit : LSB) คือบิตที่อยู่ขวามือสุดซึ่งเป็นบิตที่มีค่าประจำหลักน้อยที่สุดเช่น 110₂ บิตที่มีนัยสำคัญต่ำสุดคือ 0 มีค่าประจำหลักเป็น 2⁰ ให้สังเกตว่าค่าประจำหลักของบิตที่มีนัยสำคัญต่ำสุดจะมีค่าเป็น 2⁰ เสมอ
     การแปลงเลขฐานสิบให้เป็นฐานสองนั้นเราอาจใช้วิธีการหาร โดยให้ตัวเลขฐานสิบเป็นตัวตั้ง แล้วหารด้วยเลข 2 ไปเรื่อยๆ จนกระทั่งผลหารเป็น 0 และในการหารแต่ละครั้งต้องเขียนเศษที่ได้จากการหารไว้ หลังจากที่หารจนผลหารเป็น 0 เราจะได้เลขฐานสองที่มีค่าเท่ากับเลขฐานสิบที่เป็นตัวตั้งโดยการเขียนเศษที่ได้จากการหารแต่ละครั้งจากล่างขึ้นบน

แสดงการแปลง 29 ซึ่งเป็นเลขฐานสิบให้อยู่ในรูปเลขฐานสอง
	วิธีทำ
	2)29   1. เริ่มต้นโดยเอา 29 ตั้งแล้วหารด้วย 2 2)14 เศษ 1 2. จากข้อ 1 ได้ผลลัพธ์เป็น 14 เศษ 1 2)7_ เศษ 0 3. ผลลัพธ์จากข้อ 2 หารด้วย 2 ผลลัพธ์เป็น 7 เศษ 0 2)3_ เศษ 1 4. ผลลัพธ์จากข้อ 3 หารด้วย 2 ผลลัพธ์เป็น 3 เศษ 1 2)1_ เศษ 1 5. ผลลัพธ์จากข้อ 4 หารด้วย 2 ผลลัพธ์เป็น 1 เศษ 1 0 เศษ 1 6. ผลลัพธ์จากข้อ 5 หารด้วย 2 ผลลัพธ์เป็น 0 เศษ 1 111012 7. เมื่อหารจนกระทั่งผลหารเป็น 0 เขียนเศษทั้งหมดที่ได้จากการหารทั้งหมดเรียงกันจากล่างขึ้นบน จะได้รูปแบบของเลขฐานสองที่มีค่าเท่ากับ 2910
	(2) การแปลงเลขฐานสองเป็นฐานสิบ          การแปลงเลขฐานสองกลับเป็นเลขฐานสิบต้องอาศัยค่าประจำหลักของแต่ละบิตในเลขฐานสองที่ต้องการแปลง โดยเราจะแยกตัวเลขในแต่ละบิตมาคูณด้วยค่าประจำหลักแล้วนำผลลัพธ์จากการคูณดังกล่าวมารวมกัน จะได้เลขฐานสิบที่มีค่าตรงกับเลขฐานสองดังตัวอย่างต่อไปนี้       ตัวอย่างที่ 1 แสดงการแปลงเลข 100012 ให้อยู่ในรูปเลขฐานสิบ     100012 = (1 x 24) + (0 x 23) + (0 x 22) + (0 x 21) + (1 x 20)   = 16 + 0 + 0 + 0 +1   = 17     ตัวอย่างที่ 2 แสดงการแปลงเลข 1001112 ให้อยู่ในรูปเลขฐานสิบ     1001112 = (1 x 25) + (0 x 24) + (0 x 23) + (1 x 22) + (1 x 21) + (1 x 20)   = 32 + 0 + 0 + 4 + 2 + 1   = 39 (3) การบวกเลขฐานสอง                การบวกเลขฐานสองมีหลักการเหมือนกับการบวกเลขฐานสิบที่เราคุ้นเคย เพียงแต่ตัวเลขในแต่ละหลักของเลขฐานสองจะมีค่ามากที่สุดคือ 1 นั่นหมายความว่าในหลักใดๆ ที่มี 1 บวกกับ 1 จะได้ผลลัพธ์เป็น 0 และทดค่า 1 ไว้ในหลักถัดไปทางซ้ายดังตัวอย่างต่อไปนี้     1. การบวกเริ่มจากพิจารณาจากหลักที่มีนัยสำคัญต่ำสุดนั่นคือหลักที่ 5 2. หลักที่ 5 เป็น 1+ 0 ได้ผลลัพธ์เป็น 1 ไม่มีการทด 3. หลักที่ 4 เป็น 1+ 1 ได้ผลลัพธ์เป็น 0 ทด 1 4. หลักที่ 3 เป็น 0 + 0 ได้ 0 แต่มีการทดจากหลักที่แล้ว เมื่อบวกกับตัวทด ได้ผลลัพธ์เป็น 1ไม่มีการทด 5. หลักที่ 2 เป็น 0 + 1 ได้ผลลัพธ์เป็น 1 ไม่มีการทด 6. หลักที่ 1 ได้ผลลัพธ์เป็น 1 เหมือนเดิม ึ7. ผลลัพธ์เป็น 111012 วอย่างที่ 2 แสดงการหาค่า 1001 + 1111     วิธีทำ     1. การบวกเริ่มจากพิจารณาจากหลักที่มีนัยสำคัญต่ำสุดนั่นคือหลักที่ 5 2. หลักที่ 5 เป็น 1+ 1 ได้ผลลัพธ์เป็น 0 ทด 1 3. หลักที่ 4 เป็น 0 + 1 ได้ 1 แต่มีการทดจากหลักที่แล้ว เมื่อบวกกับตัวทด ได้ผลลัพธ์เป็น 0 และมีการทดไปยังหลักทางซ้าย 1 4. หลักที่ 3 เป็น 0 + 1 ได้ 1 แต่มีการทดจากหลักที่แล้ว เมื่อบวกกับตัวทด ได้ผลลัพธ์เป็น 0 และมีการทดไปยังหลักทางซ้าย 1 5. หลักที่ 2 เป็น 1 + 1 ได้ 0 แต่มีการทดจากหลักที่แล้ว เมื่อบวกกับตัวทด ได้ผลลัพธ์เป็น 1 และมีการทดไปยังหลักทางซ้าย 1 6. หลักที่ 1 จากตัวทดจากหลักที่แล้วได้ผลลัพธ์เป็น 1 เหมือนเดิม ึ7. ผลลัพธ์เป็น 110002

(4) การลบเลขฐานสอง
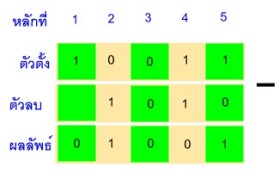
	การลบเลขฐานสองก็เช่นเดียวกับการลบเลขฐานสิบ คือพิจารณาเอาเลขที่เป็นตัวตั้งลบด้วยตัวลบทีละหลัก หากตัวตั้งเป็น 1 ตัวลบเป็น 0 ผลลัพธ์ได้เป็น 1 แต่ถ้าตัวตั้งเป็น 0 และตัวลบเป็น 1 ต้องมีการดึงค่าในหลักที่อยู่ทางซ้ายมาได้ผลลัพธ์เป็น 1 และมีผลให้ค่าของหลักที่ถูกดึงมามีค่าเป็น 0 ดังตัวอย่างต่อไปนี้ ตัวอย่างที่ 1 แสดงการหาค่า 10011 - 1010
		1. การลบเริ่มพิจารณาจากหลักที่มีนัยสำคัญต่ำสุดนั่นคือหลักที่ 5 2. หลักที่ 5 เป็น 1 - 0 ได้ผลลัพธ์เป็น 1 3. หลักที่ 4 เป็น 1 - 1 ได้ผลลัพธ์เป็น 0 4. หลักที่ 3 เป็น 0 - 0 ได้ 0 5. หลักที่ 2 เป็น 0 - 1 ต้องดึงค่าจากหลักที่อยู่ทางซ้าย คือ 10 มาช่วยเป็น 10 - 1 ได้ผลลัพธ์เป็น 1 6. หลักที่ 1 ถูกหลักที่อยู่ทางขวาดึงไป ทำให้เหลือค่าเป็น 0 7. ผลลัพธ์เป็น 10012

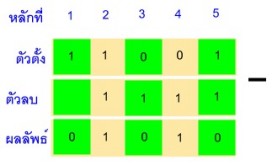
ตัวอย่างที่ 2.8  แสดงการหาค่า 11001 - 1111
		1. การลบเริ่มพิจารณาจากหลักที่มีนัยสำคัญต่ำสุดนั่นคือหลักที่ 5 2. หลักที่ 5 เป็น 1 - 1 ได้ผลลัพธ์เป็น 0 3. หลักที่ 4 เป็น 0 - 1 ต้องดึงค่าจากหลักที่อยู่ทางซ้าย คือ 10 มาช่วยเป็น 10 - 1 ได้ผลลัพธ์เป็น 1 4. หลักที่ 3 หลังจากหลักที่อยู่ทางขวาดึงค่าไป ทำให้เหลือค่าเป็น 1 และ 1-1 ได้ 0 5. หลักที่ 2 ในทำนองเดียวกับหลักที่ 3 เหลือค่า 0 ทำให้ต้องยืมค่ามาจากหลักที่ 1 เป็น 10 - 1 ทำให้ได้ผลลัพธ์เป็น 1 6. หลักที่ 1 ถูกหลักที่อยู่ทางขวาดึงไป ทำให้เหลือค่าเป็น 0 7. ผลลัพธ์เป็น 10102
	เมื่อมนุษย์สามารถแปลงเลขฐานสิบเป็นฐานสอง และแปลงเลขฐานสองกลับเป็น เลขฐานสิบได้ ก็สามารถเขียนโปรแกรมเพื่อสั่งการคอมพิวเตอร์ทำงานได้ตามที่ต้องการ และพัฒนาวิธีการในการสื่อสารหรือสั่งการคอมพิวเตอร์มาเรื่อยๆ จนในปัจจุบันผู้ใช้คอมพิวเตอร์ทั่วไปอาจไม่ต้องทำความเข้าใจการทำงานของคอมพิวเตอร์อย่างลึกซึ้งเช่นนี้ เนื่องจากมีบุคลากรที่ทำหน้าที่คิดค้นโปรแกรมที่สามารรับข้อความ หรือคำสั่งในรูปแบบของภาษาและระบบตัวเลขที่ผู้ใช้คุ้นเคย แล้วแปลความหมายเป็นเลขฐานสองก่อนส่งให้เครื่องคอมพิวเตอร์ประมวลผล

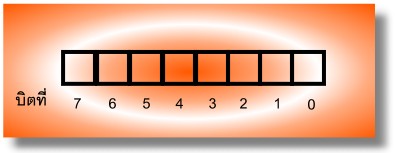
(1) รหัสแอสกี (American Standard Code Information Interchange :ASCII) เป็นมาตรฐานที่นิยมใช้กันมากในระบบคอมพิวเตอร์และระบบสื่อสารข้อมูล รหัสแทนข้อมูลชนิดนี้ใช้เลขฐานสองจำนวน 8 บิตหรือเท่ากับ 1 ไบต์แทนอักขระหรือสัญลักษณ์แต่ละตัว ซึ่ง หมายความว่าการแทนอักขระแต่ละตัวจะประกอบด้วยตัวเลขฐานสอง 8 บิตเรียงกัน ซึ่งลำดับของแต่ละบิตเป็นดังนี้
	และตัวอย่างรหัสแทนข้อมูล เช่น
	จากหลักการของระบบเลขฐานสอง แต่ละบิตสามารถแทนค่าได้ 2 แบบ คือ เลข 0 หรือเลข 1 ถ้าเราเขียนเลขฐานสองเรียงกัน 2 บิตในการแทนอักขระ เราจะมีรูปแบบในการแทนอักขระได้ 22 หรือ 4 รูปแบบ คือ 00 , 01 , 10 และ11 ดังนั้นในการใช้รหัสแอสกีซึ่งมี 8 บิตในการแทนอักขระแล้ว เราจะมีรูปแบบที่ใช้แทนได้ถึง 28 หรือ 256 รูปแบบ ซึ่งเมื่อใช้แทนตัวอักษรภาษาอังกฤษแล้วยังมีเหลืออยู่ สำนักงานมาตรฐานผลิตภัณฑ์อุตสาหกรรม หรือ สมอ. จึงได้กำหนดรหัสภาษาไทยเพิ่มลงไปเพื่อให้ใช้งานร่วมกัน ตามตารางแสดงรหัส ASCII

(2) รหัสเอ็บซิดิก (Extended Binary Coded Decimal Interchange Code : EBCDIC) พัฒนาโดยบริษัทไอบีเอ็ม รหัสแทนข้อมูลนี้ไม่เป็นที่นิยมใช้แล้วในปัจจุบัน       การกำหนดรหัสจะใช้ 8 บิต ต่อหนึ่งอักขระ เหมือนกับรหัสแอสกี แต่แบบของรหัสที่กำหนดจะแตกต่างกัน โดยรหัสเอ็บซิดิกจะเรียงลำดับแต่ละบิตที่ใช้แทนอักขระดังนี้
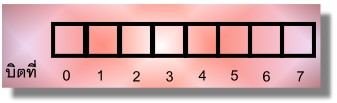	รหัสแบบเอ็บซีดิก ก็สามารถใช้กำหนดให้กับอักษรภาษาไทยและเครื่องหมายอื่นๆ ได้เช่นเดียวกัน ตัวอย่างรหัสแทนข้อมูลแบบเอ็บซีดิก
	(3) รหัสยูนิโค้ด (Unicode) เป็นรหัสที่สร้างขึ้นมาในระยะหลังที่มีการสร้างแบบตัวอักษรของภาษาต่างๆ รหัสยูนิโค้ดเป็นรหัสที่ต่างจาก 2 ชนิดที่ได้กล่าวมาข้างต้น คือใช้เลขฐานสอง 16 บิตในการแทนตัวอักษร เนื่องจากที่มาของการคิดค้นรหัสชนิดนี้ คือ เมื่อมีการใช้งานคอมพิวเตอร์ในหลายประเทศและมีการสร้างแบบตัวอักษร (font) ของภาษาต่างๆ ทั่วโลก ในบางภาษาเช่น ภาษาจีน และภาษาญี่ปุ่น เป็นภาษาที่เรียกว่าภาษารูปภาพซึ่งมีตัวอักษรเป็นหมื่นตัว หากใช้รหัสที่เป็นเลขฐานสอง 8 บิต เราสามารถแทนรูปแบบตัวอักษรได้เพียง 256 รูปแบบที่ได้อธิบายมาข้างต้น ซึ่งไม่สามารถแทนตัวอักษรได้ครบ จึงสร้างรหัสใหม่ขึ้นมาที่สามารถแทนตัวอักขระได้ถึง 65,536 ตัว ซึ่งมากพอและสามารถแทนสัญลักษณ์กราฟิกและสัญลักษณ์ทางคณิตศาสตร์ได้อีกด้วย